O que são tensões?

É a medida das forças internas que atuam em um corpo sendo deformado pela ação de uma força.

Quando é aplicado uma força de tração em uma barra de aço por exemplo, o material tende a “esticar” apresentando deformação gradual à medida que a força vai aumentando.

Deformação é qualquer mudança da geometria de um determinado corpo após a aplicação de uma força externa. Se trata de uma medida adimensional que correlaciona o tamanho inicial com o tamanho final da geometria. Em um ensaio de tração, a deformação pode ser medida por:

Quais são os tipos de tensão? Tensão normal, flexão, cisalhamento...

Basicamente existem componentes de tração e compressão que atuam em cada molécula constituinte dos materiais, nada mais do que isso. Entretanto as combinações dos tipos de tensão podem ocasionar tensões de flexão e cisalhamento também. Como resumo:

• A tensão normal é relativa a efeitos puramente de tração ou compressão (produzem deformação em um plano normal de aplicação da força) – aplicando uma força de tração em uma régua, o material tende a se “esticar” resultando em tensões e deformações de tração;

• A tensão de flexão é relativa aos efeitos de tração e compressão em uma mesma seção transversal – aplicando uma força que faça a régua fletir para baixo por exemplo, é gerado uma tensão de tração na face superior e compressão na face inferior, como mostram as imagens abaixo:
  • O vetor vermelho representa tração e o azul representa compressão:

• A tensão de cisalhamento existe quando duas partes do material tendem a deslizar uma contra o outra – imagine aplicar 01 força cortante bem próximo ao local que a régua esteja engastada (fixa);
  • As tensões principais relativas ao cisalhamento se dão a 45º do eixo horizontal, como mostra a imagem abaixo:

Figura 1 - exemplo de cisalhamento

O que é estado uniaxial, plano e triplo de tensão?

O estado de tensão em um ponto do material é o conjunto de todas as tensões ocorrendo em todos os planos passando pelo ponto.

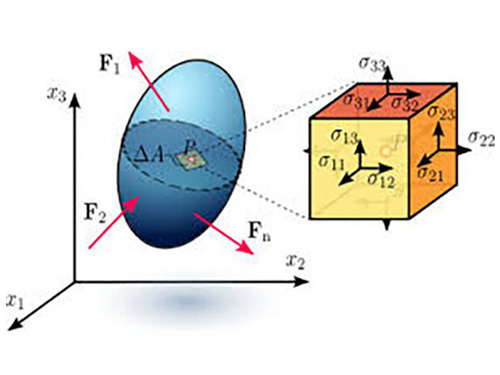
O intuito é definir quais são as tensões atuantes em cada ponto do material, sendo que podemos analisar os resultados de tensão em um volume infinitesimal, como mostra a imagem abaixo:

O estado uniaxial é quando existe uma componente da tensão sendo considerada em apenas uma direção (ex. ensaio de tração);

Figura 2 - estado uniaxial de tensão

Estado plano de tensão é quando são consideradas as tensões atuantes em todas as direções de um plano, portanto nesse caso as tensões de cisalhamento atuantes no plano já são levadas em consideração.

Um exemplo prático de estado plano de tensão são chapas onde a espessura é muito pequena quando comparada com o comprimento. As tensões ao longo da espessura podem ser desprezadas, sendo um caso de estado plano de tensão:

Estado triplo de tensão admite a existência de tensões em todas as direções de um volume infinetisimal, levando em consideração as 09 componentes necessárias para definir o tensor de tensão;

Um exemplo prático para estado triplo de tensão são peças grossas e robustas como fundidas e forjadas onde suas dimensões são consideráveis em todas as direções, existindo portanto tensões consideráveis em todas as direções.

Na realidade, todas as solicitações causam tensões em todas as direções e, portanto, poderiam ser classificadas como estado triplo de tensão. Na prática por existirem casos em que as tensões são mínimas em determinadas direções, as simplificações para estado plano ou uniaxial são realizadas.

Diante das afirmações acima, você deve estar se perguntando como é possível correlacionar todas as tensões atuantes em um ponto de modo que se previna a falha do componente.

O primeiro passo importante é caracterizar o material como dúctil ou frágil, pois a partir daí é possível identificar se o material vai falhar por escoamento ou por tração.

Materiais frágeis falham por conta das tensões normal (tração e/ou compressão), onde a fratura é abrupta e o material não tem poder de se deformar antes da ruptura (ductilidade).

Materiais dúcteis falham por conta das tensões de escoamento, onde a fratura ocorre após o escoamento do material, sendo característico a formação de “pescoço”, características dos aços carbono por exemplo.

Figura 3 - exemplo de fratura dúctil na imagem (a) e frágil na imagem (b)

Diante da necessidade de combinar o estado de tensão em um ponto do material, aliado as características dos materiais, surgiram os critérios de falha para os tipos de materiais, sendo os mais conhecidos de Tresca, Von Mises e Rankine.

Critério de Tresca

Utilizando a ideia de que os materiais Dúcteis falham por cisalhamento, Henri Tresca propôs em 1868 a sua teoria que é usada para prever a tensão de falha de um material dúctil submetido a qualquer tipo de carregamento.

Essa teoria considera que o escoamento do material começa quando a tensão de cisalhamento máxima absoluta atinge o valor da tensão de cisalhamento que provoca escoamento do material em um ensaio de tração.

A tensão máxima de cisalhamento ocorre na maior diferença entre as tensões principais, portanto pode ser calculado por:

A tensão de Tresca pode ser calculada a partir das tensões principais, como também está disponível na maioria dos software de Elementos Finitos.

Considerando a equação apresentada acima, em um estado plano de tensões, denominando a tensão principal de σ1 no eixo x e a mínima de σ2 no eixo y de um elemento infinitesimal,  podemos representar graficamente o critério de Tresca da seguinte maneira:

Repare que a região mais crítica está localizada no quadrante 2 e 4, onde as tensões principais possuem sinais opostos e são somadas para fornecer o valor da tensão equivalente. Essa equação nos evidencia que o caso de maior tensão de cisalhamento, é onde existe a maior diferença de valores de tensão considerando 02 direções, ou seja, caso você esteja realizando um cálculo em uma determinada peça de material dúctil e estiver considerando as tensões em apenas 01 direção, muitas vezes pode não estar obtendo os valores das máximas tensões de cisalhamento e dessa maneira, realizando o cálculo de maneira equivocada.

Critério de Von Mises

A teoria de von Mises é também utilizada para materiais dúcteis, apresentando resultados melhores com dados experimentais e, desse modo, é geralmente mais utilizado nas validações estruturais.

O critério de Von Mises leva em consideração os conceitos de energia de distorção de um elemento, que também pode ser interpretado como a energia necessária para que ocorra mudança de forma em um elemento.

Esse critério define que um elemento estrutural (dúctil) irá falhar se a energia associada à mudança de forma de um corpo, submetido a um carregamento multiaxial, ultrapassar a energia de distorção de um corpo de prova submetido a um ensaio uniaxial de tração.

A tensão equivalente de Von Mises, pode ser calculada por:

Para casos de estado plano de tensão, podemos considerar a parcela de σ2 = 0, resultando na equação abaixo:

Graficamente, podemos representar a equação como:

Figura 4 - critério de Von Mises

Comparando os critérios de Tresca e Von Mises, podemos analisar que o critério de Tresca é mais conservador, uma vez que a área traçada dentro dos limites estipulados pela sua equação é menor do que a área estipulado pela equação de Von Mises.

Figura 5 - comparativo do criterios

Teoria da tensão normal máxima Rankine

Materiais frágeis tendem a falhar subitamente por fratura sem escoamento aparente. Em um teste de tração, a fratura ocorre quando a tensão normal atinge o limite de resistência, essa teoria estabelece nada mais que um material frágil falha quando a tensão principal máxima σ  atinge um valor limite igual ao limite de resistência que o material suporta quando submetido a tração simples. Essa teoria é válida para materiais frágeis cujos diagramas tensão-deformação sejam similares tanto sob tração quanto sobre compressão.

Portanto o critério de Rankine, pode ser utilizado considerando as equações abaixo:

Figura 6 - Teoria da tensão normal máxima – Rankine

Alguns termos importantes:

Elasticidade – é a capacidade do material retornar ao seu estado inicial após a finalização de um carregamento, não apresentando deformações residuais;

Plasticidade – é a deformação que não retorna ao seu estado inicial após a finalização de um carregamento, apresentando deformações residuais.

Ductilidade – capacidade do material a se deformar antes da ruptura. Quanto mais dúctil o aço, maior é a redução da área da seção transversal do corpo de prova, como também o alongamento.

Resiliência – capacidade de absorver energia mecânica no regime elástico, ou seja, a capacidade de restituir a energia mecânica absorvida.

Tenacidade – capacidade de absorção de energia mecânica em regime elástico e plástico. É representada pela área total do diagrama tensão-deformação, sendo sua unidade (J/m³), ou seja, é a energia total que o material pode absorver até a ruptura, por unidade de volume.

Dureza – é a resistência oferecida pela superfície a penetração de uma peça de maior dureza;

Estricção – é a redução das dimensões da seção transversal, provocada pela carga de tração aplicada ao material.

Resistência a tração – é a máxima tensão aplicada ao corpo de prova relativa a máxima carga de tração aplicada.

Soldabilidade – é a capacidade de adequação a soldagem que o material oferece.

Temperabilidade – é a susceptibilidade de endurecimento por resfriamento rápido, ou a propriedade, nas ligas ferrosas, que determina a profundidade e a distribuição da dureza produzida por uma tempera. Descrevendo fisicamente, podemos definir como a capacidade de um aço transformar total ou parcialmente de austenita para algum percentual de martensita a uma profundidade quando resfriado sob certas condições. Aumentando o limite a resistência a tração e da dureza, reduzindo a ductilidade e tenacidade dos materiais, aparecendo também tensões internas.

Esse artigo foi útil para você? Deixe seu comentário e compartilhe com seus colegas.

Caso tenha alguma dúvida, estamos à disposição para ajudá-lo.

Abraço,