INTRODUÇÃO
Os tanques industriais são equipamentos cujo sua principal função é o armazenamento de fluídos diversos, podendo ser empregado em muitas etapas do processo produtivo industrial, nos mais variados ramos da indústria.
São exemplos de aplicação de tanques na indústria:
1. Armazenamento de produtos acabados e/ou produtos intermediários;
2. Armazenamento de insumos e/ou resíduos;
3. Armazenamento de matérias primas.
Diversos são os tipos, tamanhos e as formas de construção dos tanques, os mais comuns são do tipo cilíndricos posicionados verticalmente ou horizontalmente, podendo ser também abertos ou fechados para a atmosfera.

Figura 1 - Exemplo de um tanque cilíndrico vertical
OBJETIVO
O objetivo desse artigo é apresentar quais são as normas necessárias para embasar as análises de elementos finitos de tanques industriais, como também todas as considerações das cargas atuantes no equipamento a fim de garantir que esta análise seja a mais fidedigna possível com as solicitações da realidade, bem como os possíveis modos de falha que o equipamento pode sofrer. Ao final será apresentada uma análise com resultados de um exemplo de avaliação de tanques utilizando o Software Ansys 2022 R2.
NORMA API 650
A norma API-650 da associação comercial (American Petroleum Institute) tem por objetivo fundamentar alguns requisitos mínimos para os materiais, projeto, fabricação, içamento e inspeção de tanques com formatos cilíndricos verticais que tenham as chapas soldadas. Estes equipamentos também devem ter o seu fundo completamente apoiado na base, e sua pressão interna não deve exceder a força peso do teto do tanque, ou não exceder 18Kpa, o que for menor. Já para pressões maiores deve-se atentar a alguns requisitos adicionais prescritos em norma.
**Para maiores informações sobre os tipos de tanques e especificidades que a norma abrange é sugerido a leitura da norma na íntegra.
CARGAS
As cargas que devem ser ponderadas nas análises de elementos finitos são retiradas do capítulo 5.2.1 da Norma API-650 2020 e estão apresentadas abaixo:
1. Peso total do tanque: Peso do equipamento juntamente com os componentes que nele estão fixados.
2. Pressão Externa: Pressão com magnitude de 0,25KPa aplicada nas chapas do costado do tanque.
3. Pressão do Fluido: Carga devido ao enchimento a nível de projeto do tanque.
4. Carga mínima no telhado: A norma estipula um valor mínimo de 0,72Kpa a ser aplicado horizontalmente na superfície do teto, caso houver.
**Outras normas como NBR 7821 estipulam este valor na escala de 60kgf/m². Já para norma técnica da Sabesp NTS231 de tanques para armazenamento de água determinam o valor de 1,0KPa.
5. Vento: Cargas relacionadas a força do vento sobre a estrutura do tanque. As cargas de vento sobre a estrutura em cada região do Brasil podem ser encontradas através da norma NBR 6123. Temos um artigo em nosso site sobre uma visão geral sobre o assunto clicando aqui.
Demais condições de cargas não serão apontadas neste artigo ou por não fazerem parte dos fenômenos naturais do nosso país (Brasil) ou não são aplicados nas combinações das cargas propostas.
COMBINAÇÕES
Continuando na norma API 650 2020 ela sugere algumas combinações de cargas no item 5.2.2 em que o projeto do tanque deve seguir. Para este artigo proposto faremos citação a duas combinações específicas a fim de verificar que o caso mais crítico acontece na combinação 01 para a análise das máximas tensões e na combinação 02 para a carga crítica de flambagem.
Sendo assim, as combinações utilizadas serão:
| Item | Combinação |
| 01 | PP + PF + SC |
| 02 | PP + VT + SC + 0,4PE |
Tabela 1 - Combinações utilizadas
Legenda:
• PP – Peso Próprio + Componentes Fixados
• VT – Vento
• PF – Pressão do Fluido
• PE – Pressão Externa
• SC – Sobrecarga
**Nota: Não exatamente a norma propõe as combinações citadas na Tabela 1, no caso da combinação 01 utilizaremos a sobrecarga no teto invés da pressão interna sugerida na norma, já que o equipamento analisado neste artigo será adotado à pressão atmosférica. Já para a combinação 02 foi somado ainda a carga relativa ao vento, sendo assim a análise que irá utilizá-la ficará ainda mais criteriosa em seus resultados.
MÉTODO DE AVALIAÇÃO
Para avaliar as tensões em tanques de armazenamento pelo método dos elementos finitos, a norma API 650 não nos indica uma forma por métodos próprios, para isto ela pondera que avaliações de acordo com as normas WRC 297 ou ASME Seção VIII Div.2 são validas para verificações das tensões nos bocais e casco cilíndrico. Pode ser encontrado esta indicação no capítulo P.3.1.1 da norma API 650 2020. Também é indicado que o tanque deva passar por uma avaliação de flambagem em sua carcaça conforme aponta o capítulo 5.6.1.4 da API 650. Temos um artigo falando sobre como a norma ASME Seção VIII Div.2 aponta sua categorização para avaliação das tensões e avaliação de flambagem, clique aqui para ver este artigo.
GEOMETRIA
Seguindo para o modelo utilizado como estudo, a seguir pode ser conferida algumas dimensões do equipamento, uma vista geral e as espessuras adotadas.
Tabela 2 - Dimensões do equipamento
| Costado | |
| Diâmetro | 2200mm |
| Altura | 3750mm |
| Tampo Superior | |
| Altura | 275mm |
| Ângulo | 14,5° |
Figura 2 - Vista das dimensões
Tabela 3 - Resumo das espessuras utilizados
| COMPONENTES | ESPESSURAS UTILIZADAS [mm] |
| Tampo Superior | 1,80 |
| Costado | 2,00 |
| Fundo | 1,89 |
| Bocais | 2,43 |
Figura 3 - Vista isométrica do equipamento
MATERIAL
De forma resumida as propriedades do material utilizado para a simulação de elementos finitos podem ser observadas na tabela 4, todos os componentes do tanque foram considerados como sendo de Aço Inox do tipo SA-240 Tp. 304.
| Material | SA-240 TP 304 (60°C) |
| Densidade [g/cm³] | 8,03 |
| Módulo de Elasticidade [GPa] | 195,12 |
| Coef. Poisson | 0,31 |
| Limite de Escoamento Sy (Min) – [MPa] | 188,60 |
| Resistência a Tração Sta (Min) – [MPa] | 506,33 |
| Eficiência de Solda (E1) | 1,00 |
| Eficiência de Fundição (E2) | 1,00 |
| Sm [MPa] | 128,00 |
| Pm [MPa] | 128,00 |
| Pl [MPa] | 193,00 |
| Pl + Pb [MPa] | 193,00 |
| Pl + Pb + Q [MPa] | 385,00 |
Tabela 4 – Propriedades do material
**As propriedades do material foram verificadas de acordo com a ASME seção II parte D, levando em consideração a temperatura de operação como sendo de (60°C) para a obtenção de suas características.
APLICAÇÃO DAS CARGAS
A aplicação das cargas já discutido anteriormente estão apresentadas nas imagens abaixo. O líquido armazenado neste exemplo foi adotado como sendo água.
Figura 4 – Gravidade relativa ao peso próprio e cargas do vento
Figura 5 – Pressão externa e sobrecarga no teto
Tabela 5 – Densidade do líquido
| Densidade - Água | 9,97e-7 kg/mm³ |
| Altura da Coluna | Totalmente cheio |
Figura 6 – Pressão do fluido
RESTRIÇÕES
As restrições aplicadas nas sapatas representam a fixação do tanque em uma fundação civil, por isto foram adotados como sendo restrição do tipo “Fixed Support”. Para o fundo do tanque foi considerado a restrição do tipo “Displacement”, restringindo o movimento do equipamento no sentido Y, enquanto X e Z são livres, representando o fundo apenas apoiado, conforme sistema de coordenadas da Figura 7.
Figura 7 – Restrições utilizadas
RESULTADOS
Chegou a hora de avaliar os resultados obtidos nas combinações mencionadas na Tabela 1. Os resultados serão apresentados da seguinte forma:
1. Combinação 01 – Referente a análise de Colapso Plástico do material.
2. Combinação 02 – Referente a análise de Flambagem do equipamento.
COMBINAÇÃO 01 – COLAPSO PLÁSTICO
De acordo com a Norma ASME seção II parte D, as tensões admissíveis adotadas são listadas na Tabela 6.
| Critério | Tensão Admissível (Mpa) |
| Primaria Membrana Generalizada (Pm [Mpa]) | 128,00 |
| Primaria Membrana Localizada (Pl [Mpa]) | 193,00 |
| Primaria Membrana Localizada + Flexão (Pl + Pb [Mpa]) | 193,00 |
| Secundária Membrana + Flexão (Pl + Pb [Mpa]) | 385,00 |
Tabela 6 – Tensões Admissíveis
• Tensão Primária de Membrana Generalizada (Pm)
Figura 8 - Vista geral das tensões primárias de membrana generalizada
Figura 9 – Vista ISO das tensões primárias de membrana generalizada acima de 128MPa
Não são observadas tensões primárias de membrana generalizada acima do limite admissível (128 MPa). Conforme pode ser observado nas imagens acima, todas as tensões resultantes atendem o critério de aceite conforme o código ASME. Portanto, os resultados são ACEITÁVEIS para este critério. As regiões com tensão acima do limite admissível serão analisadas como tensão primaria de membrana localizada.
• Tensão primária de membrana localizada (Pl)
Figura 10 - Vista geral das tensões primárias de membrana localizadas
Figura 11 – Vista ISO das tensões primárias de membrana localizada acima de 193 MPa
Como pode ser observado as tensões primárias de membrana localizada estão em níveis abaixo do limite admissível (193 MPa). Conforme pode ser observado nas imagens acima, todas as tensões resultantes atendem o critério de aceite conforme o código ASME. Portanto, os resultados são ACEITÁVEIS para este critério.
• Tensão primária de membrana + Flexão (Pl+Pb)
Figura 12 - Vista geral das tensões primárias de membrana + flexão
Figura 13 – Vista ISO das tensões primárias de membrana + flexão acima de 193 MPa
Não são observadas tensões primárias de membrana + flexão acima do limite admissível (193 MPa). Conforme pode ser observado nas imagens acima, todas as tensões resultantes atendem o critério de aceite conforme o código ASME. Portanto, os resultados são ACEITÁVEIS para este critério. As regiões acima do limite admissível serão analisadas como tensões secundárias.
• Tensão Secundária (Q)


Conforme podem ser observadas as tensões secundárias se encontram em níveis abaixo do limite admissível (385 MPa). Conforme pode ser observado nas imagens acima, todas as tensões resultantes atendem o critério de aceite conforme o código ASME. Portanto, os resultados são ACEITÁVEIS para este critério.
COMBINAÇÃO 02 – FLAMBAGEM
Considerando a pressão negativa atuante no costado devido a cargas que contribuam para este fenômeno acontecer, o fator de redução de capacidade de flambagem é:
Bcr = 0,8
O fator de segurança para a prevenção da flambagem é calculado por:
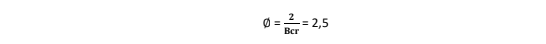
A carga crítica de flambagem calculada pela análise de elementos finitos é mostrada abaixo:
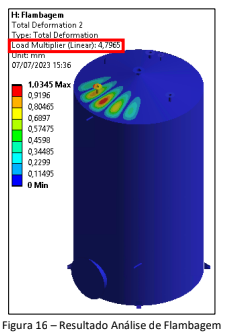
Conforme observado na figura acima o equipamento em questão se encontra com níveis aceitáveis para o critério de flambagem.
CONCLUSÃO
Este artigo teve como objetivo mostrar de forma simplificada o modo de avaliação de tanques de armazenamento utilizando a norma API 650 2020 como referência de carregamentos, e das combinações que devemos ponderar em nossa análise de elementos finitos.
Observamos também que não existe exatamente uma repartição na norma API 650 que regulamenta avaliações por método computacional dos elementos finitos, sugerindo assim que sigamos colocações da norma ASME VIII div. 2, por exemplo.
De forma geral conforme observado nos resultados do equipamento exemplo no decorrer deste artigo, tanto para a avaliação da combinação 01 (colapso plástico) quanto para combinação 02 (flambagem) nosso modelo estaria APTO a prosseguir com sua operação normalmente. Ou seja, operar com segurança em sua capacidade máxima, sem que nenhum tipo de modificação seja necessário.
Gostou do artigo? Tem algum comentário ou vivência sobre o assunto?
Fique à vontade em deixar seu comentário abaixo.
O Fatigue Tool é uma ferramenta do Ansys Workbench que permite fazer o cálculo de fadiga dos modelos analisados. Através dele é possível determinar:
A fadiga é a principal responsável pela falha de equipamentos e componentes mecânicos, e é de conhecimento de todos que os cálculos para verificação de fadiga levam um certo tempo e trabalho para serem feitos.
Uma maneira rápida e prática de se realizar os cálculos de fadiga é através do Fatigue Tool do Ansys Workbench, onde é possível utilizar os resultados de tensão da análise de elementos finitos para calcular a vida de fadiga de um componente.
Este artigo possui o intuito de mostrar exclusivamente um pouco mais sobre a ferramenta Fatigue Tool. Se você possui interesse em aprender um pouco mais sobre fadiga recomendamos a playlist de fadiga do nosso canal no Youtube e os demais artigos referentes a esse tema:
Para mostrar essa ferramenta utilizamos o pedal de freio da equipe EESC USP Fórmula SAE. O modelo do pedal em CAD é mostrado abaixo:
Figura 1 - Montagem do pedal (modelo original)
Como pode ser visto na imagem o modelo é fixado pela parte inferior do pedal, além disso o pedal conta com dois cilindros fixados na haste responsável por acionar o sistema hidráulico, como mostra a imagem abaixo:
Figura 2 - Vista em corte do cilindro mestre com a presença do pedal.
Considerando que o objetivo principal da análise é realizar o cálculo de fadiga do pedal do freio, não foi necessário levar o conjunto completo do sistema.
Figura 3 - Modelo utilizado na análise de elementos finitos.
O material aplicado ao modelo pode ser visto na imagem abaixo:
Figura 4 - Material aplicado ao modelo.
As propriedades mecânicas do material são detalhadas na tabela abaixo:
Tratando-se de uma análise de fadiga, é necessário realizar a configuração adequada entrando com o número de ciclos e tensão alternada, como mostra a imagem abaixo:
Figura 5 - Dados da curva de fadiga e curva de fadiga construída pelo Ansys (escala logarítimica), respectivamente.
Os pontos mostrados acima, foram calculados de acordo com a equação da curva S-N e dados de fadiga do material encontrados no eFatigue:
Figura 6 - Curva de fadiga S-N (Fonte: eFatigue).
A configuração da curva de fadiga deve ser feita acessando o “Engineering Data” da análise em questão, e selecionando a opção “S-N curve”.
Figura 7 - Detalhe do Engineering Data.
Figura 8 - Forma de inserir a curva S-N.
Os contatos do modelo podem ser vistos na imagem abaixo:
Figura 9 - Contato entre o pedal e a chapa onde o piloto pisa.
A malha do modelo é mostrada abaixo:
Figura 10 - Vista isométrica da malha do modelo.
Figura 11 - Vista lateral e frontal da malha, respectivamente.
Foram aplicadas 02 restrições no modelo, sendo a primeira referente a rotula inferior e outra relativa ao cilindro mestre.
Figura 12 - Detalhe da restrição Remote Dispacement aplicada ao modelo.
A máxima tensão desse pedal ocorre o momento em que o cilindro atinge o fim de curso, pois a partir desse momento não existe mais liberdade para ele se movimentar e acontece um efeito de alavanca no pedal.
Figura 13 - Condição de restrição representando a compressão total do cilindro (fixo em Y).
A força aplicada ao pedal foi de 2kN.
Figura 14 - Força de cálculo aplicada ao modelo.
Os resultados obtidos na análise estática são os seguintes:
Figura 15 - Vista isométrica do deslocamento do modelo e vista lateral do modelo ampliada, respectivamente.
Figura 16 - Vista geral das tensões de von-Mises do modelo - vista isométrica e lateral, respectivamente.
A máxima tensão no modelo ocorre no raio inferior de alívio, como pode ser observado na imagem abaixo:
Figura 17 - Detalhe da máxima tensão de von-Mises.
Uma das principais dificuldades da análise de fadiga, é entender se a tensão máxima é realmente coerente e pode ser considerada para o cálculo.
Quando se realiza uma análise para prevenir o colapso plástico é normal que as tensões máximas sejam desprezadas e que seja considerado uma tensão distante do ponto máximo, levando em consideração o fato de que um ponto de tensão muito localizada mesmo que ultrapassar o limite de escoamento vai se redistribuir e não ocasionará uma falha por colapso plástico.
Entretanto para a falha por fadiga justamente esses pontos localizados de tensão é que são os grandes causadores da iniciação e propagação da trinca.
Por este motivo, nesta região foi realizado uma análise de convergência para verificar se a tensão de ~440MPa é real e pode ser considerada para o cálculo de fadiga.
O processo de convergência pode ser realizado automaticamente pelo Ansys, clicando com o botão direito em cima do resultado de tensão e selecionando a opção “Convergence”, conforme é mostrado abaixo:
Figura 18 - Forma de inserir o comando Convergence.
Quando essa opção é ativada, o Ansys resolve a análise de maneira iterativa e compara os resultados das tensões obtidas. A cada iteração a malha é refinada para verificar se existe um aumento de tensão dentro uma % pré determinada.
A porcentagem de mudança permitida pode ser definida pelo usuário no local destacado abaixo:
Figura 19 - Verificação da convergencia.
Ao final do processo iterativo é possível verificar a malha final do modelo:
Figura 20 - Detalha da região de máxima tensão com malha refinada.
As tensões da análise estática podem ser comparadas com o limite de escoamento para identificar o coeficiente de segurança do projeto.
Como pode ser observado a tensão atuante é bem próxima ao limite de escoamento gerando um coeficiente de segurança de 14%.
O primeiro passo é inserir o Fatigue Tool da mesma maneira que são inseridos os resultados da análise, como mostrado abaixo:
Figura 21 - Local onde deve ser inserido o Fatigue Tool.
Posteriormente, é necessário definir alguns parâmetros:
Figura 22 - Detalhes do Fatigue Tool.
Os parâmetros definidos para essa análise foram:
Para a análise de fadiga desse modelo foram inseridos os resultados do número de ciclos e coeficiente de segurança, como pode ser visto nas imagens abaixo:
Figura 27 - Vista de fadiga do componente, vista isométrica e detalhe da região de menor vida, respectivamente.
Figura 28 - Vista dos coeficiente se segurança do pedal e vista iso das regiões com CS menores que 1, respectivamante.
A tensão máxima obtida no pedal do freio é alta e gerou uma vida de fadiga muito baixa ~25 pisadas no freio com a força de 2KN.
O método utilizado para o cálculo de fadiga foi o S-N que é apropriado para fadiga de alto ciclo (acima de 10.000 ciclos), e, portanto, não é válido para os resultados obtidos. Entretanto, considerando que o intuito seja projetar um componente para fadiga de alto ciclo é válido que esse método seja utilizado para verificar se o design está apropriado ou não.
Portanto, neste caso é necessário realizar modificações na geometria e rodar novamente a análise para obter novos resultados.
Como pode ser observado é rápido e prático utilizar a ferramenta Fatigue Tool para o cálculo de fadiga, no entanto, como em qualquer análise, deve-se sempre tomar cuidado com os parâmetros de input e análise dos resultados.
Algo que também é um ponto positivo, sem dúvidas é o fato do Mechanical apresentar uma parte gráfica que permite observar os resultados através da escala de cores, isso ajuda a perceber os pontos de menor coeficiente de segurança e trabalhar de maneira rápida para corrigir o necessário, modificando o design e rodando iterações.
Gostou do artigo? Deixe seu comentário.
A necessidade de medir torque em equipamentos pode ser dos mais variados, podendo estar relacionado com investigação de falha, determinação da potência mecânica ou até de maneira preventiva.
Para ilustrar o procedimento de medição de torque em eixos vamos utilizar um tubo em que será possível fazer a instalação dos sensores como também a validação dos resultados dos testes através da análise de elementos finitos.
Figura 1 - Teste experimental de torque e análise de elementos finitos, respectivamente.
Neste teste, os extensômetros foram posicionados no meio do tubo e uma força pré determinada foi aplicada na haste para produzir um torque conhecido.
Figura 2 - Setup para teste de torque.
O sensor utilizado para a medição do torque é o extensômetro (ou strain gauge) que mede a deformação superficial do material quando submetido a carregamentos externos. Se quiser aprender mais sobre os extensômetros, acesse nosso artigo: Extensômetria (Strain Gauge) - O que é? Quando utilizar?
Para esta aplicação é necessário utilizar a configuração de ponte completa, onde são instalados 4 extensômetros para a obtenção de um resultado de torque.
Os extensômetros utilizados são do tipo espinha de peixe, em que a grade do sensor é disposta a 45° da linha horizontal, conforme imagem abaixo:
Figura 3 - Extensômetro do tipo "espinha de peixe".
Essa disposição é por conta da direção da deformação principal de um elemento submetido puramente a torção ser de exatamente 45° em relação ao eixo longitudinal, conforme imagem abaixo:
Figura 4 - Direção das máximas deformações principais.
Foram posicionados 02 extensômetros do tipo “espinha de peixe” defasados 180° um em relação ao outro, conforme é mostrado na imagem abaixo:
Figura 5 - Vista isométrica do tubo com referências das vistas.
Figura 6 - Detalhe com posicionamento dos extensômetros.
Figura 7 - Detalhe com posicionamento dos extensômetros.
Figura 8 - Psicionamento longitudinal do extensômetro.
Figura 9 - Psicionamento radial dos extensômetros (180°).
Figura 10 - Psicionamento dos extensômetros (top e bottom).
Após o posicionamento dos sensores, toda a ligação e cabeamento foi realizada:
Figura 11 - Cabeamento e conector.
Para coleta de dados foram utilizados equipamentos National Instruments, sendo o chassi cDAQ-9191 e Módulo de aquisição NI 9237.
Figura 12 - Chassis cDAQ-9191 e módulo NI-9237.
O cabo RJ50 foi conectado ao módulo NI-9237, como mostra a imagem abaixo:
Figura 13- Conexão entre o cabo RJ50 e módulo NI-9237.
O resultado do teste é apresentado abaixo:
Figura 14 - Gráfico de Deformação x Tempo.
Levando em consideração que o tubo apresenta deformações dentro da zona elástica e aplicando a Lei de Hooke para transformar deformação em tensão, considerando o módulo de elasticidade como 200GPa, temos:
Figura 15 - Gráfico de Tensão x Tempo.
Considerando a mesma carga e condição de restrição, os resultados da análise de elementos finitos são apresentados abaixo:
Figura 16 - Condições de restrição para análise de elementos finitos.
Figura 17 - Vista ISO com o resultado da tensão de cisalhamento.
A comparação entre o teste experimental e a análise de elementos finitas é apresentada na tabela abaixo:
O interessante desse tipo de instalação é que o resultado obtido é referente apenas a torção no tubo, e as deformações relativas a outras solicitações (ex. flexão, tração ou compressão) não são medidas pela maneira que os extensômetros estão dispostos no componente. Isso se torna muito interessante para aplicações onde é necessário medir apenas o torque de um eixo ou algum componente que esteja submetido a torção.
Ficou alguma dúvida sobre esse tipo de instalação ou tem alguma aplicação em que seja interessante esse tipo de medição? Compartilhe conosco e deixe seu comentário abaixo.
Nesse artigo vamos detalhar o planejamento e obtenção das forças a serem consideradas em uma análise estrutural utilizando o método dos elementos finitos em um Pórtico giratório, considerando os requisitos da norma NBR8400.
Passo 01)
Primeiramente é necessário entender o movimento do pórtico. Para o exemplo mostrado abaixo, é possível avaliar que se trata de um pórtico giratório que possui uma viga caixão, uma torre circular e um sistema de giro, conforme imagem abaixo:
Figura 1 - pórtico analisado
Figura 2 - detalhe dos rolamentos e sistema de giro
Passo 02)
Posteriormente é necessário obter as informações de operação do Pórtico – essas informações geralmente são disponibilizadas em desenhos ou catálogos de fabricação do pórtico. Em último caso, essas informações podem ser obtidas com o time de campo que acompanha o funcionamento do equipamento.
Para este exemplo, os dados do pórtico giratório são disponibilizados abaixo:
Passo 03)
O próximo passo é classificar a estrutura do pórtico de acordo com a norma NBR8400. Para isso, é necessário acessar a tabela 01, 02, 03 e 04 de acordo com as imagens abaixo:
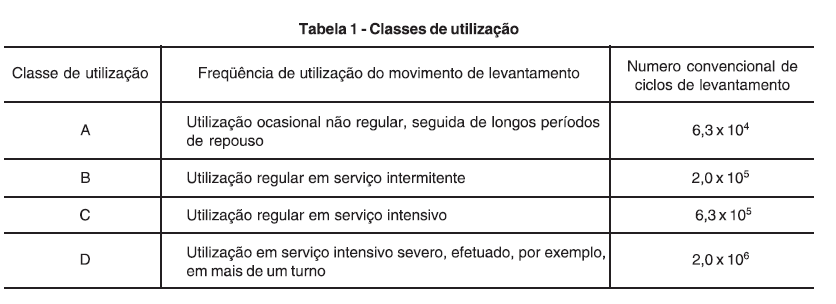
Figura 3 - tabela 01 da norma NBR8400
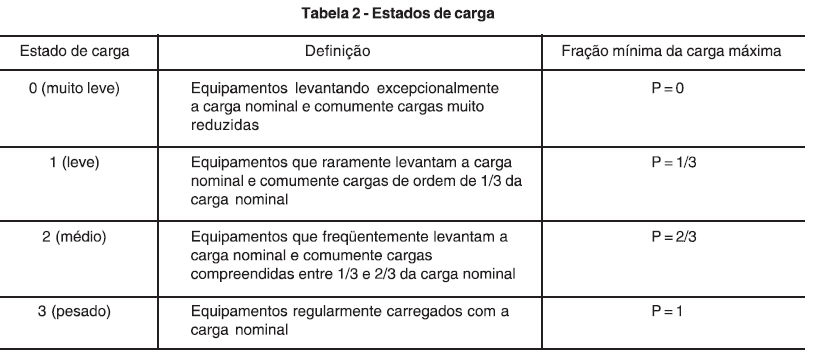
Figura 4 - tabela 02 da norma NBR8400
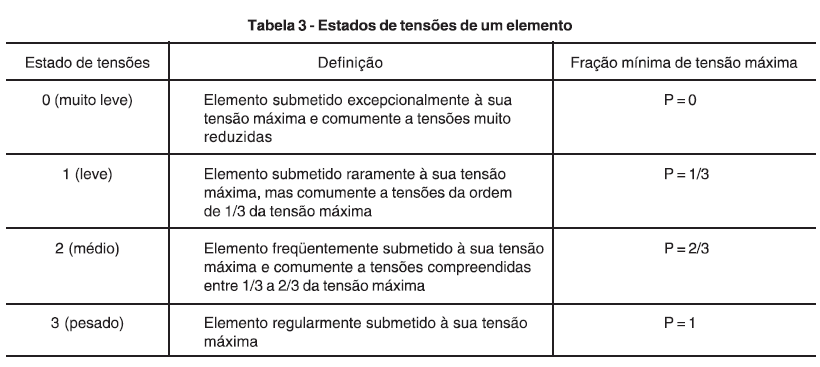
Figura 5 - tabela 03 da norma NBR8400
Figura 6 - tabela 04 da norma NBR8400
Para o exemplo do pórtico giratório, tem-se:
Passo 04)
Definição das solicitações principais, de acordo com o item 5.5.1 da norma NBR8400. As cargas podem ser divididas basicamente entre verticais e horizontais:
Solicitações Verticais:
Deve-se definir o coeficiente dinâmico a ser aplicado na carga de serviço através da tabela 05 da norma NBR8400.
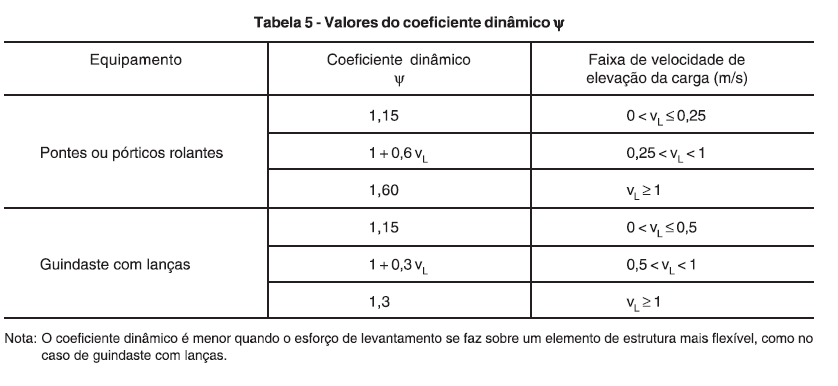
Figura 7 - tabela 05 da norma NBR8400
De acordo com as informações obtidas no passo 02 para esse pórtico temos uma velocidade de elevação de carga de 5m/min (0,0833m/s) gerando um coeficiente dinâmico de 1,15.
![]()
Adicionalmente é necessário calcular o coeficiente de majoração dado pela tabela 10 ou 11 da norma NBR 8400.
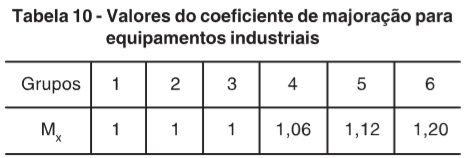
Figura 8 - coeficiente de majoração - tabela 10

Figura 9 - tabela 11 - coeficiente de majoração para equipamentos utilizados em siderúrgicas e grupo 06
Para o pórtico em questão, o coeficiente de majoração é:
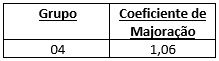
O cálculo das solicitações verticais deve ser calculado pelo maior resultado das equações abaixo:
Ocorre que para a análise de elementos finitos, a carga de peso próprio é contabilizada pelo efeito da gravidade, sendo que o peso próprio a ser contabilizado nas equações deve ser somente o peso dos equipamentos que não serão contabilizados pelo efeito da gravidade.
Para o pórtico em questão, o peso próprio que não está sendo contabilizado na equação é o da talha, sendo, portanto:
As forças verticais serão majoradas posteriormente nos casos de combinações das cargas, entretanto com o intuito de ficar mais visual e prático, a força calculada é mostrada na imagem abaixo sendo aplicada na região mais distante do pórtico, gerando dessa maneira o maior momento fletor na viga caixão.
Figura 10 - força vertical Fv (os valores não estão corretos pois ainda serão majorados na próxima seção)
Solicitações Horizontais:
As forças horizontais são resultantes de várias condições de operação do equipamento, sendo detalhadas abaixo:
Para Fh1:
Para o pórtico em questão:
Essa força é calculada a partir da massa a movimentar dos elementos móveis e deve ser aplicada nos caminhos de rolamento, na direção paralela a ele.
Para o pórtico em questão:
Figura 11 - força de aceleração e desaceleração do trole (os valores não estão corretos pois ainda serão majorados na próxima seção)
2. O movimento de rotação da viga, pode ser calculado por:
Nesse caso, a massa a se movimentar é toda a viga + peso da talha, portanto:
Figura 12 - volume da viga do pórtico
Calculando a velocidade tangencial da “lança”, temos:
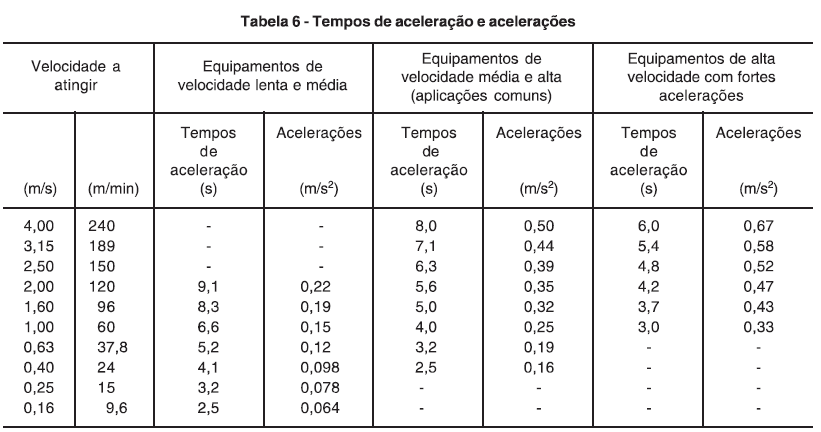
Com base na velocidade tangencial, os valores de velocidade de translação e aceleração são obtidos na tabela 06 da NBR8400:
Para o pórtico em questão:
Essa força é oriunda da aceleração/desaceleração da viga em torno do “poste” – note que a viga possui rotação livre em torno do “poste”, e, portanto, aplicar a força na face lateral da viga não faz sentido. Na realidade o que acontece é que no momento de uma aceleração/desaceleração essa força é transferida para o eixo de rotação e será transferida diretamente para o poste. Dessa maneira a força foi aplicada diretamente na região do eixo, como é mostrado abaixo:
Figura 13 - força de aceleração/desaceleração do giro do pórtico (os valores não estão corretos pois ainda serão majorados na próxima seção)
Para Fh2:
O cálculo da força centrífuga não é muito bem explorado pela norma no caso de Pórticos, e dessa maneira os cálculos foram realizados tomando como base a equação física dessa força, dada por:
Note que o raio da força centrífuga para desbalanceamentos rotativos, é a distância do centro de massa ao eixo de giro, dessa maneira o raio nesse caso é:
Figura 14 - raio da força centrífuga
A direção dessa força é no sentido radial de acordo com a imagem abaixo:
Figura 15 - definição da direção da força centrífuga
A força centrífuga do pórtico pode ser calculada por:
Essa força deve ser aplicada no sentido radial para fora, na tampa externa da viga, de acordo com a imagem abaixo. Note que o local de aplicação da força não é o mais adequado, entretanto o efeito mais importante é o momento gerado no “Poste” central.
Figura 16 - força centrífuga (os valores não estão corretos pois ainda serão majorados na próxima seção)
Para Fh3:
O caso das reações horizontais transversais é devido a forças de reação que as rodas fazem nos trilhos. Dessa maneira essa força é perpendicular ao caminho de rolamento, sendo calculada através da definição de um coeficiente (ξ) e dependendo da relação entre o vão e a distância entre eixos (v/a).
O coeficiente (ξ) é determinado através da Figura 03 da norma NBR 8400.
Figura 17 - gráfico para a determinação do coeficiente
Para o pórtico em questão:
Figura 18 - distância entre eixos do trole
Figura 19 - vão do pórtico
Note que a relação v/a é superior ao fornecido na figura 3.
Ocorre que para o Pórtico em questão essa força não deve ser aplicada, levando em consideração os motivos abaixo:
Para Fh4:
Os choques podem ocorrer na carga suspensa ou na estrutura, sendo distinguidos entre os casos em que a carga suspensa pode oscilar, e quando não pode oscilar.
Algumas informações importantes:
Para o pórtico em questão:
A carga é oscilante com velocidade de translação inferior a 0,7m/s.
Para Fh5:
A pressão aerodinâmica é determinada por:
O esforço devido a ação do vento em uma viga é uma força cujo componente na direção do vento é calculada por:
Para o pórtico em questão:
Figura 20 - área para o cálculo da força do vento
Figura 21 - tabela 08 da norma NBR8400
Utiliza-se o maior coeficiente aerodinâmico – como os dois coeficientes são iguais, o utilizado é 1,4.
Figura 22 - tabela 07 da norma NBR8400
Considerando que a altura máxima do pórtico é de 9,564m (~10m) o vento é dado por:
A força do vento é calculada por:
Essa força deve ser aplicada perpendicularmente a área mostrada acima.
Figura 23 - força do vento aplicada na estrutura do Pórtico (condição de serviço)
Figura 24 - força do vento aplicada na estrutura do Pórtico (equipamento fora de serviço)
A norma NBR8400 ainda prevê uma carga de vento a ser aplicada na carga suspensa, estabelecendo áreas indicativas para o cálculo dessa força do vento atuando nas cargas suspensas, sendo:
Dessa maneira, para o pórtico em questão:
Calculando a força do vento na carga suspensa:
A força devido a carga suspensa é aplicada na região do Trole, de acordo com as imagens abaixo:
Figura 25 - força do vento devido a carga suspensa (condição de serviço)
Figura 26 - força do vento devido a carga suspensa (equipamento fora de serviço)
Passo 05)
Determinar os casos de solicitação de acordo com o item 5.6 da norma.
Antes de entrarmos nos casos, é recomendado que se faça um resumo de todas as forças calculadas. Para o pórtico em questão temos:
Caso I:
Para o FEA, temos:
Caso II:
Obs – a força do vento não é majorada pelo coeficiente de majoração.
Para o FEA, temos:
Caso III:
Considera-se a pior das situações abaixo:
Para o pórtico em questão, considerando que não existe o efeito de choque, temos:
Sendo que:
Portanto, existem 02 situações que devem ser analisadas:
Pronto, as forças e casos foram calculados de acordo com a NBR8400 sendo a próxima etapa referente a rodar os cálculos e avaliar os resultados. Caso exista alguma dúvida, ou se quiserem mais artigos sobre a análise de elementos finitos em equipamentos de levantamento de carga, deixe seu comentário abaixo!
Obrigado,
A base é uma das etapas do método de Elementos Finitos, ou seja, o que você precisa fazer desde possuir a geometria em CAD até obter os resultados. Também comentamos sobre as várias áreas existentes dentro da análise de Elementos Finitos – conhecer esses conceitos é de extrema importância para você analisar as várias aplicabilidades do método, como também ter ideia de como essa área é vasta.
Para você que quer aprender Elementos Finitos, mas não tem software:
O Ansys disponibiliza a versão acadêmica que deve ser utilizada para fins educacionais. No último slide da aula, comento um pouco sobre como fazer o download do software.
Compartilhe com seus colegas e deixe seu comentário no vídeo.
Leia mais sobre Elementos Finitos.
Quando e porque: é curioso saber quais são as áreas e situações em que a análise de Elementos Finitos é utilizada. Confesso que até hoje ficamos surpreso com os casos e solicitações que aparecem para a Ensus – temos muito interesse e motivação em descobrir sempre mais onde podemos utilizar essa ferramenta.
Preparamos um vídeo sobre quando e porque utilizar a análise de Elementos Finitos. Separamos os principais motivos, como também utilizamos casos reais para explicar cada caso.
Compartilhe com seus colegas e deixe seu comentário no vídeo.
Leia mais sobre Elementos Finitos.
