INTRODUÇÃO
Os tanques industriais são equipamentos cujo sua principal função é o armazenamento de fluídos diversos, podendo ser empregado em muitas etapas do processo produtivo industrial, nos mais variados ramos da indústria.
São exemplos de aplicação de tanques na indústria:
1. Armazenamento de produtos acabados e/ou produtos intermediários;
2. Armazenamento de insumos e/ou resíduos;
3. Armazenamento de matérias primas.
Diversos são os tipos, tamanhos e as formas de construção dos tanques, os mais comuns são do tipo cilíndricos posicionados verticalmente ou horizontalmente, podendo ser também abertos ou fechados para a atmosfera.

Figura 1 - Exemplo de um tanque cilíndrico vertical
OBJETIVO
O objetivo desse artigo é apresentar quais são as normas necessárias para embasar as análises de elementos finitos de tanques industriais, como também todas as considerações das cargas atuantes no equipamento a fim de garantir que esta análise seja a mais fidedigna possível com as solicitações da realidade, bem como os possíveis modos de falha que o equipamento pode sofrer. Ao final será apresentada uma análise com resultados de um exemplo de avaliação de tanques utilizando o Software Ansys 2022 R2.
NORMA API 650
A norma API-650 da associação comercial (American Petroleum Institute) tem por objetivo fundamentar alguns requisitos mínimos para os materiais, projeto, fabricação, içamento e inspeção de tanques com formatos cilíndricos verticais que tenham as chapas soldadas. Estes equipamentos também devem ter o seu fundo completamente apoiado na base, e sua pressão interna não deve exceder a força peso do teto do tanque, ou não exceder 18Kpa, o que for menor. Já para pressões maiores deve-se atentar a alguns requisitos adicionais prescritos em norma.
**Para maiores informações sobre os tipos de tanques e especificidades que a norma abrange é sugerido a leitura da norma na íntegra.
CARGAS
As cargas que devem ser ponderadas nas análises de elementos finitos são retiradas do capítulo 5.2.1 da Norma API-650 2020 e estão apresentadas abaixo:
1. Peso total do tanque: Peso do equipamento juntamente com os componentes que nele estão fixados.
2. Pressão Externa: Pressão com magnitude de 0,25KPa aplicada nas chapas do costado do tanque.
3. Pressão do Fluido: Carga devido ao enchimento a nível de projeto do tanque.
4. Carga mínima no telhado: A norma estipula um valor mínimo de 0,72Kpa a ser aplicado horizontalmente na superfície do teto, caso houver.
**Outras normas como NBR 7821 estipulam este valor na escala de 60kgf/m². Já para norma técnica da Sabesp NTS231 de tanques para armazenamento de água determinam o valor de 1,0KPa.
5. Vento: Cargas relacionadas a força do vento sobre a estrutura do tanque. As cargas de vento sobre a estrutura em cada região do Brasil podem ser encontradas através da norma NBR 6123. Temos um artigo em nosso site sobre uma visão geral sobre o assunto clicando aqui.
Demais condições de cargas não serão apontadas neste artigo ou por não fazerem parte dos fenômenos naturais do nosso país (Brasil) ou não são aplicados nas combinações das cargas propostas.
COMBINAÇÕES
Continuando na norma API 650 2020 ela sugere algumas combinações de cargas no item 5.2.2 em que o projeto do tanque deve seguir. Para este artigo proposto faremos citação a duas combinações específicas a fim de verificar que o caso mais crítico acontece na combinação 01 para a análise das máximas tensões e na combinação 02 para a carga crítica de flambagem.
Sendo assim, as combinações utilizadas serão:
| Item | Combinação |
| 01 | PP + PF + SC |
| 02 | PP + VT + SC + 0,4PE |
Tabela 1 - Combinações utilizadas
Legenda:
• PP – Peso Próprio + Componentes Fixados
• VT – Vento
• PF – Pressão do Fluido
• PE – Pressão Externa
• SC – Sobrecarga
**Nota: Não exatamente a norma propõe as combinações citadas na Tabela 1, no caso da combinação 01 utilizaremos a sobrecarga no teto invés da pressão interna sugerida na norma, já que o equipamento analisado neste artigo será adotado à pressão atmosférica. Já para a combinação 02 foi somado ainda a carga relativa ao vento, sendo assim a análise que irá utilizá-la ficará ainda mais criteriosa em seus resultados.
MÉTODO DE AVALIAÇÃO
Para avaliar as tensões em tanques de armazenamento pelo método dos elementos finitos, a norma API 650 não nos indica uma forma por métodos próprios, para isto ela pondera que avaliações de acordo com as normas WRC 297 ou ASME Seção VIII Div.2 são validas para verificações das tensões nos bocais e casco cilíndrico. Pode ser encontrado esta indicação no capítulo P.3.1.1 da norma API 650 2020. Também é indicado que o tanque deva passar por uma avaliação de flambagem em sua carcaça conforme aponta o capítulo 5.6.1.4 da API 650. Temos um artigo falando sobre como a norma ASME Seção VIII Div.2 aponta sua categorização para avaliação das tensões e avaliação de flambagem, clique aqui para ver este artigo.
GEOMETRIA
Seguindo para o modelo utilizado como estudo, a seguir pode ser conferida algumas dimensões do equipamento, uma vista geral e as espessuras adotadas.
Tabela 2 - Dimensões do equipamento
| Costado | |
| Diâmetro | 2200mm |
| Altura | 3750mm |
| Tampo Superior | |
| Altura | 275mm |
| Ângulo | 14,5° |
Figura 2 - Vista das dimensões
Tabela 3 - Resumo das espessuras utilizados
| COMPONENTES | ESPESSURAS UTILIZADAS [mm] |
| Tampo Superior | 1,80 |
| Costado | 2,00 |
| Fundo | 1,89 |
| Bocais | 2,43 |
Figura 3 - Vista isométrica do equipamento
MATERIAL
De forma resumida as propriedades do material utilizado para a simulação de elementos finitos podem ser observadas na tabela 4, todos os componentes do tanque foram considerados como sendo de Aço Inox do tipo SA-240 Tp. 304.
| Material | SA-240 TP 304 (60°C) |
| Densidade [g/cm³] | 8,03 |
| Módulo de Elasticidade [GPa] | 195,12 |
| Coef. Poisson | 0,31 |
| Limite de Escoamento Sy (Min) – [MPa] | 188,60 |
| Resistência a Tração Sta (Min) – [MPa] | 506,33 |
| Eficiência de Solda (E1) | 1,00 |
| Eficiência de Fundição (E2) | 1,00 |
| Sm [MPa] | 128,00 |
| Pm [MPa] | 128,00 |
| Pl [MPa] | 193,00 |
| Pl + Pb [MPa] | 193,00 |
| Pl + Pb + Q [MPa] | 385,00 |
Tabela 4 – Propriedades do material
**As propriedades do material foram verificadas de acordo com a ASME seção II parte D, levando em consideração a temperatura de operação como sendo de (60°C) para a obtenção de suas características.
APLICAÇÃO DAS CARGAS
A aplicação das cargas já discutido anteriormente estão apresentadas nas imagens abaixo. O líquido armazenado neste exemplo foi adotado como sendo água.
Figura 4 – Gravidade relativa ao peso próprio e cargas do vento
Figura 5 – Pressão externa e sobrecarga no teto
Tabela 5 – Densidade do líquido
| Densidade - Água | 9,97e-7 kg/mm³ |
| Altura da Coluna | Totalmente cheio |
Figura 6 – Pressão do fluido
RESTRIÇÕES
As restrições aplicadas nas sapatas representam a fixação do tanque em uma fundação civil, por isto foram adotados como sendo restrição do tipo “Fixed Support”. Para o fundo do tanque foi considerado a restrição do tipo “Displacement”, restringindo o movimento do equipamento no sentido Y, enquanto X e Z são livres, representando o fundo apenas apoiado, conforme sistema de coordenadas da Figura 7.
Figura 7 – Restrições utilizadas
RESULTADOS
Chegou a hora de avaliar os resultados obtidos nas combinações mencionadas na Tabela 1. Os resultados serão apresentados da seguinte forma:
1. Combinação 01 – Referente a análise de Colapso Plástico do material.
2. Combinação 02 – Referente a análise de Flambagem do equipamento.
COMBINAÇÃO 01 – COLAPSO PLÁSTICO
De acordo com a Norma ASME seção II parte D, as tensões admissíveis adotadas são listadas na Tabela 6.
| Critério | Tensão Admissível (Mpa) |
| Primaria Membrana Generalizada (Pm [Mpa]) | 128,00 |
| Primaria Membrana Localizada (Pl [Mpa]) | 193,00 |
| Primaria Membrana Localizada + Flexão (Pl + Pb [Mpa]) | 193,00 |
| Secundária Membrana + Flexão (Pl + Pb [Mpa]) | 385,00 |
Tabela 6 – Tensões Admissíveis
• Tensão Primária de Membrana Generalizada (Pm)
Figura 8 - Vista geral das tensões primárias de membrana generalizada
Figura 9 – Vista ISO das tensões primárias de membrana generalizada acima de 128MPa
Não são observadas tensões primárias de membrana generalizada acima do limite admissível (128 MPa). Conforme pode ser observado nas imagens acima, todas as tensões resultantes atendem o critério de aceite conforme o código ASME. Portanto, os resultados são ACEITÁVEIS para este critério. As regiões com tensão acima do limite admissível serão analisadas como tensão primaria de membrana localizada.
• Tensão primária de membrana localizada (Pl)
Figura 10 - Vista geral das tensões primárias de membrana localizadas
Figura 11 – Vista ISO das tensões primárias de membrana localizada acima de 193 MPa
Como pode ser observado as tensões primárias de membrana localizada estão em níveis abaixo do limite admissível (193 MPa). Conforme pode ser observado nas imagens acima, todas as tensões resultantes atendem o critério de aceite conforme o código ASME. Portanto, os resultados são ACEITÁVEIS para este critério.
• Tensão primária de membrana + Flexão (Pl+Pb)
Figura 12 - Vista geral das tensões primárias de membrana + flexão
Figura 13 – Vista ISO das tensões primárias de membrana + flexão acima de 193 MPa
Não são observadas tensões primárias de membrana + flexão acima do limite admissível (193 MPa). Conforme pode ser observado nas imagens acima, todas as tensões resultantes atendem o critério de aceite conforme o código ASME. Portanto, os resultados são ACEITÁVEIS para este critério. As regiões acima do limite admissível serão analisadas como tensões secundárias.
• Tensão Secundária (Q)


Conforme podem ser observadas as tensões secundárias se encontram em níveis abaixo do limite admissível (385 MPa). Conforme pode ser observado nas imagens acima, todas as tensões resultantes atendem o critério de aceite conforme o código ASME. Portanto, os resultados são ACEITÁVEIS para este critério.
COMBINAÇÃO 02 – FLAMBAGEM
Considerando a pressão negativa atuante no costado devido a cargas que contribuam para este fenômeno acontecer, o fator de redução de capacidade de flambagem é:
Bcr = 0,8
O fator de segurança para a prevenção da flambagem é calculado por:
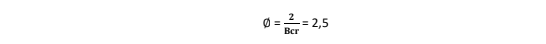
A carga crítica de flambagem calculada pela análise de elementos finitos é mostrada abaixo:
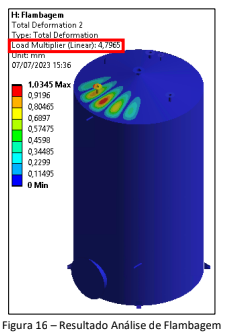
Conforme observado na figura acima o equipamento em questão se encontra com níveis aceitáveis para o critério de flambagem.
CONCLUSÃO
Este artigo teve como objetivo mostrar de forma simplificada o modo de avaliação de tanques de armazenamento utilizando a norma API 650 2020 como referência de carregamentos, e das combinações que devemos ponderar em nossa análise de elementos finitos.
Observamos também que não existe exatamente uma repartição na norma API 650 que regulamenta avaliações por método computacional dos elementos finitos, sugerindo assim que sigamos colocações da norma ASME VIII div. 2, por exemplo.
De forma geral conforme observado nos resultados do equipamento exemplo no decorrer deste artigo, tanto para a avaliação da combinação 01 (colapso plástico) quanto para combinação 02 (flambagem) nosso modelo estaria APTO a prosseguir com sua operação normalmente. Ou seja, operar com segurança em sua capacidade máxima, sem que nenhum tipo de modificação seja necessário.
Gostou do artigo? Tem algum comentário ou vivência sobre o assunto?
Fique à vontade em deixar seu comentário abaixo.
